嗨,开发者们,
感知器是机器学习中最简单和最基本的概念之一。它是一种二元线性分类器,是神经网络的基础。在这篇文章中,我将逐步讲解如何从零开始在Python中理解和实现感知器。
让我们开始吧!
什么是感知器?
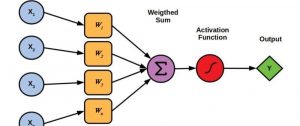
感知器是一种用于二元分类器的监督学习基本算法。给定输入特征,感知器学习权重,以帮助根据简单的阈值函数分离类别。以下是其简单工作原理:
- 输入:特征向量(例如,
[x1, x2])。 - 权重:每个输入特征都有一个权重,模型根据其性能调整这些权重。
- 激活函数:计算输入特征的加权和,并应用阈值来决定结果属于哪个类别。
在数学上,它看起来像这样:
f(x) = w1*x1 + w2*x2 + … + wn*xn + b
其中:
- f(x)是输出,
- w表示权重,
- x表示输入特征,
- b是偏置项。
如果 f(x) 大于或等于一个阈值,则输出为类别 1;否则,输出为类别 0。
第一步:导入库
我们这里只使用 NumPy 进行矩阵运算,以保持轻量级。
import numpy as np
第二步:定义感知器类
我们将把感知器构建为一个类,以保持一切有序。该类将包括用于训练和预测的方法。
class Perceptron:
def __init__(self, learning_rate=0.01, epochs=1000):
self.learning_rate = learning_rate
self.epochs = epochs
self.weights = None
self.bias = None
def fit(self, X, y):
# 样本数量和特征数量
n_samples, n_features = X.shape
# 初始化权重和偏置
self.weights = np.zeros(n_features)
self.bias = 0
# 训练
for _ in range(self.epochs):
for idx, x_i in enumerate(X):
# 计算线性输出
linear_output = np.dot(x_i, self.weights) + self.bias
# 应用阶跃函数
y_predicted = self._step_function(linear_output)
# 如果发生误分类,则更新权重和偏置
if y[idx] != y_predicted:
update = self.learning_rate * (y[idx] - y_predicted)
self.weights += update * x_i
self.bias += update
def predict(self, X):
# 计算线性输出并应用阶跃函数
linear_output = np.dot(X, self.weights) + self.bias
y_predicted = self._step_function(linear_output)
return y_predicted
def _step_function(self, x):
return np.where(x >= 0, 1, 0)在上面的代码中:
-
fit:该方法通过调整权重和偏差来训练模型,每当模型错误分类一个点时就进行调整。
-
predict:该方法对新数据进行预测计算。
-
_step_function:该函数应用阈值来确定输出类别。
第3步:准备一个简单的数据集
我们将使用一个小数据集,以便于可视化输出。以下是一个简单的与门数据集:
# 与门数据集
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 0, 0, 1]) # 与门的标签第4步:训练和测试感知器
现在,让我们训练感知器并测试其预测结果。
# 初始化感知器
p = Perceptron(learning_rate=0.1, epochs=10)
# 训练模型
p.fit(X, y)
# 测试模型
print("预测结果:", p.predict(X))
与门的预期输出:
预测结果: [0 0 0 1]
感知器学习过程的解释
- 初始化权重和偏置:在开始时,权重被设置为零,这使得模型能够从头开始学习。
- 计算线性输出:对于每个数据点,感知器计算输入的加权和加上偏置。
- 激活(阶跃函数):如果线性输出大于或等于零,则分配类1;否则,分配类0。
- 更新规则:如果预测不正确,模型会调整权重和偏置,以减少误差的方向。更新规则如下:权重 += 学习率 * (真实值 – 预测值) * 输入
这使得感知器仅对错误分类的点进行更新,逐渐将模型推向正确的决策边界。
可视化决策边界
在训练后可视化决策边界。这在处理更复杂的数据集时尤其有帮助。在上面,我们使用了简单的与门。
扩展到多层感知器(MLPs)
虽然感知器仅限于线性可分问题,但它是更复杂的神经网络(如多层感知器(MLPs))的基础。在MLPs中,我们添加隐藏层和激活函数(如ReLU或Sigmoid)来解决非线性问题。
总结
感知器是一个简单但基础的机器学习算法。通过理解它的工作原理并从零实现,我们可以深入了解机器学习和神经网络的基础。感知器的美在于其简单性,使其成为任何对人工智能感兴趣的人的完美起点。


